Do k-Sparse Autoencoders Reveal Thinking Patterns? Interpretable Features in a Small Reasoning Model
This article explores whether k-Sparse Autoencoders, a specific type of models used primarily for Mechanistic Interpretability, are able to extract interpretable features related to the thinking process of a small reasoning model. Through experimenting with DeepSeek R1 Distill Qwen 1.5B and EleutherAI's k-SAEs, it was found that certain latent features strongly activate in response to tokens used by the model in the reasoning process.
Overview
Problem Statement
Models such as sparse autoencoders (SAEs) and k-sparse autoencoders have been used as an effective medium to extract meaningful interpretable features from neural networks, including Large Language Models (LLMs). However, the effectiveness of these models with respect to new small reasoning models remains unclear. While it may seem obvious that it’s possible to extract features from reasoning models using SAEs, it’s not fully determined whether they can effectively uncover features, especially in small reasoning models. In addition, an interesting question arises when thinking about the nature of reasoning models: Do reasoning models have specific features that relate to the thinking process that it performs?
This project aims to investigate whether k-sparse autoencoders are capable of extracting features from a small reasoning model, with a focus on finding evidence for features that correspond to the reasoning process of the model. Providing evidence to answer this question could support the presence of interpretable features related to the model’s reasoning process, in addition to possibly enhancing our comprehension of small reasoning models.
Principal Takeaways
- The trained k-Sparse Autoencoders that were used effectively extracted features from DeepSeek R1 Distill Qwen 1.5B.
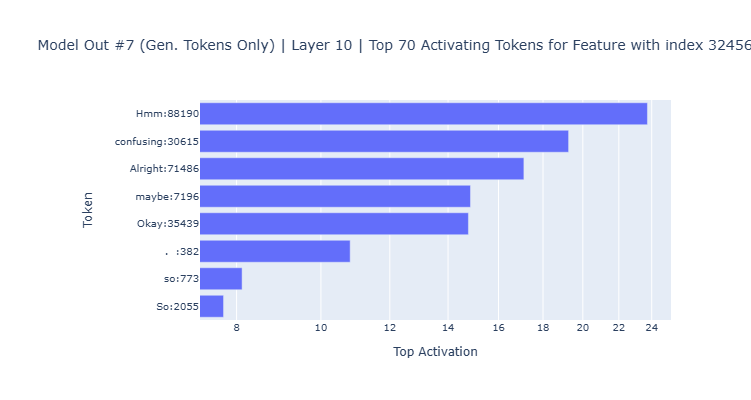
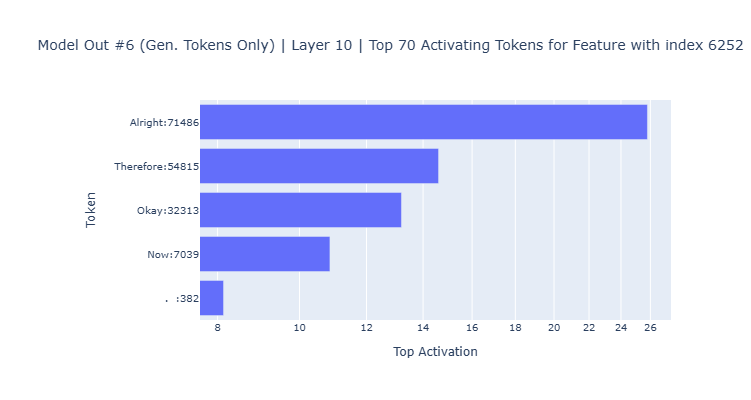
- The analysis of the latent activations obtained from the SAEs encoder showed there were several features, such as features 32456, 6252 and 31146 in layer 10, that strongly activate with tokens related to the reasoning process of the model.
- There are features that have top activations with several different tokens that seem complicated to interpret, possibly due to the lack of a direct relationship between them.
- There are also features that have top activations with few different tokens, indicating that they possibly have specialized focus or that they are selective, responding to specific tokens.
While the results are promising, I have to say that there is room for opportunities to further analyse the feature activations or refine the analysis methodology to enhance feature extraction accuracy and interpretation.
Key Experiments
The main experiment consisted of first generating 32 model inferences with problems from the GSM8K dataset, using a temperature of 0.6 and a maximum of 400 new (generated) tokens. The hidden states of these inferences were encoded using a k-sparse autoencoder (k = 32) focusing on three layers: 5, 10 and 20, thus obtaining the top 32 latent activations and feature indices per inference and layer.
The first hidden state (related to the input prompt tokens) was excluded because of what is seems to be a model bias towards the ”<|begin▁of▁sentence|>” and ”<|User|>” special tokens and to maintain a focus on the model generated tokens.
Then, an analysis of the latent activations and feature indices was performed by obtaining the top feature activations, feature and activation frequencies per layer and model inference, in addition to the top activating tokens per feature, layer and inference. Several graphs were created to visualize and analyze this.
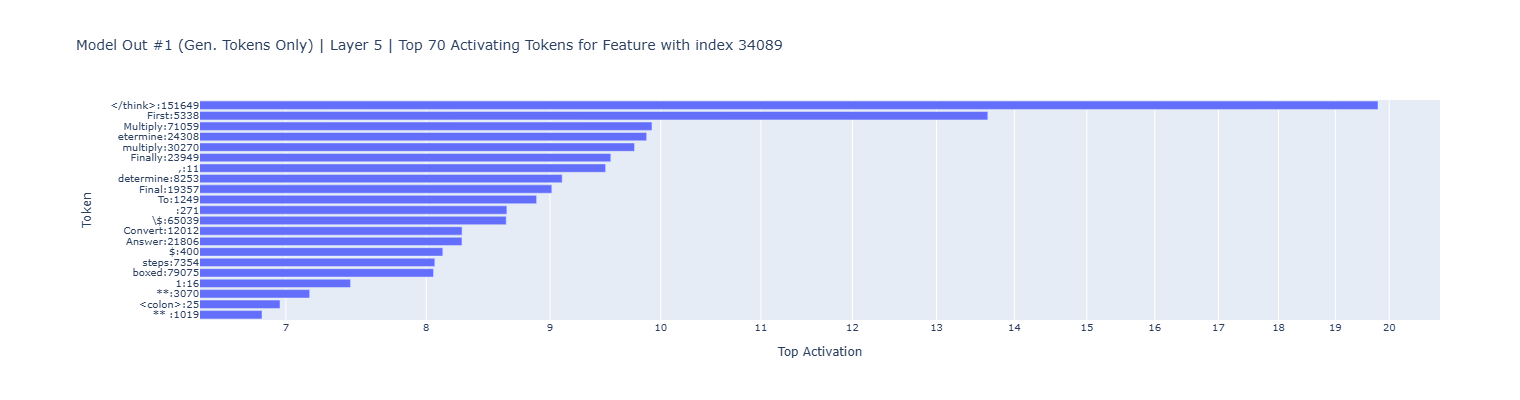
The graphs below are examples of a plausible relationship between tokens the model commonly uses within the reasoning process. The feature 32456 was a top feature for 28 model inferences, feature 6252 for 14 inferences, and feature 31146 for 10 inferences. All of these features appear in layer 10, also indicating the importance of this layer for the reasoning process.
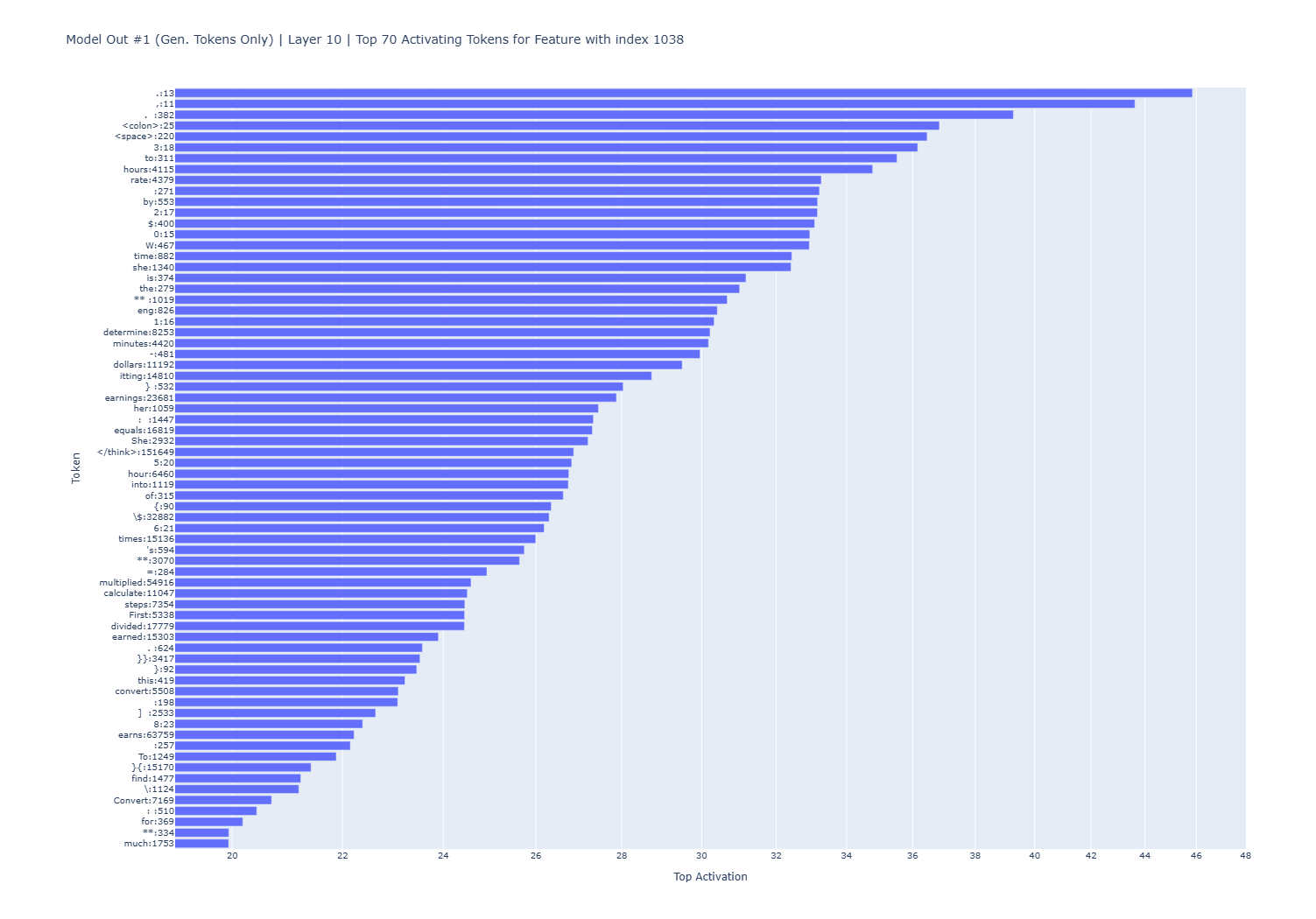
This experiment also revealed the presence of features with a large number of varied top activating tokens, as well as features with a small number of specific activating tokens. The following graph shows an example of one feature (feature 1038 in layer 10, was a top feature in 32 inferences) with high activation values related to several tokens that don’t seem to have a direct and specific relationship.
The code that was developed for this project can be found in this GitHub repository.
Development Process
Resources
These are the resources that were used to conduct the experiments in this project:
- DeepSeek R1 Distill Qwen 1.5B for the small reasoning model.
- The GSM8K (Grade School Math 8K) dataset.
- EleutherAI’s SAE DeepSeek R1 Distill Qwen 1.5B 65k trained k-sparse autoencoder (k = 32). According to EleutherAI’s sparsify GitHub repository, the k-sparse autoencoder was trained roughly following the methodology described in Scaling and evaluating sparse autoencoders (Gao et al. 2024).
The main reasons behind the reasoning model and dataset selection involve effectively running the experiments until completion within the coding environment I currently have access to, in addition to the time constraints this project needs to fulfill.
Preliminary Analysis and Experiments with Model Inference
All the inferences of the model were generated with a temperature of 0.6 and a maximum of 400 new (generated) tokens. The input prompts were formatted using a chat template to make the model behave like an assistant. Furthermore, the prompt format follows the recommendations given in the DeepSeek R1 model card with just a small change:
Raw input reasoning prompt example:
<|begin▁of▁sentence|><|User|>2 + 3 = x What is the value of x? Please reason step by step in a few words, and put your final answer within \\boxed{}<|Assistant|><think>\n
As we can see, the prompt ends with “<think>” followed by a “\n” token to ensure that the model responds using the thinking or reasoning process.
Model output example (formatted for readability):
<|begin▁of▁sentence|><|User|>Weng earns $12 an hour for babysitting. Yesterday, she just did 50 minutes of babysitting. How much did she earn? Please reason step by step in a few words, and put your final answer within \boxed{}<|Assistant|><think>
To determine how much Weng earned from babysitting, I need to multiply her hourly rate by the time she worked. She earns $12 per hour and worked for 50 minutes.
First, I’ll convert 50 minutes into hours by dividing by 60. This gives me approximately 0.8333 hours.
Next, I’ll multiply the hourly rate of $12 by 0.8333 hours to find her total earnings.
</think>
To determine how much Weng earned from babysitting, follow these steps:
- Hourly Rate:
Weng earns $12 per hour.
- Time Worked:
She babysat for 50 minutes.
- Convert Minutes to Hours:
Since there are 60 minutes in an hour, convert 50 minutes to hours:
- Calculate Earnings:
Multiply the hourly rate by the time worked in hours:
Final Answer:
<|end▁of▁sentence|>
In this example, the model’s reasoning is slightly more general, focusing more on the logic behind the problem, and then determining a possible plan, along with some non-explicit “calculations”, to get to a solution. Then the model applies this logic to generate its final response.
An interesting observation to notice is that the wording the model uses during the thinking process is relatively similar across multiple responses. Words such as “hmm”, “okay”, “alright”, and similar thinking expressions appear quite frequently. This can be seen in the following examples of fragments from the model’s thinking process (the line breaks were applied for readability in both examples).
Model’s thinking process fragment example #1 (formatted for readability):
<|begin▁of▁sentence|><|User|>2 + x = 10 What is the value of x? Please reason step by step in a few words, and put your final answer within \boxed{}<|Assistant|><think>
Okay, so I have this equation here: 2 plus x equals 10. Hmm, I need to find the value of x. Alright, let me think about how to approach this. I remember from class that when you have an equation like this, you want to isolate the variable, which in this case is x.
So, the equation is 2 + x = 10. I need to get x by itself on one side of the equation. To do that, I should get rid of the 2 that’s being added to x. How do I do that? Well, the opposite of addition is subtraction, right? So if I subtract 2 from both sides of the equation, that should help me isolate x.
Let me write that out step by step. Starting with 2 + x = 10, if I subtract 2 from both sides, it should look like this:
2 + x - 2 = 10 - 2
Simplifying both sides, the 2 and -2 on the left side cancel each other out, leaving just x. On the right side, 10 minus 2 is 8. So that gives me x = 8.
Wait, let me double-check that to make sure I didn’t make a mistake.
…
Model’s thinking process fragment example #2 (formatted for readability):
<|begin▁of▁sentence|><|User|>Natalia sold clips to 48 of her friends in April, and then she sold half as many clips in May. How many clips did Natalia sell altogether in April and May? Please reason step by step in a few words, and put your final answer within \boxed{}<|Assistant|><think>
Alright, so I have this problem here about Natalia selling clips. Let me read it again: “Natalia sold clips to 48 of her friends in April, and then she sold half as many clips in May. How many clips did Natalia sell altogether in April and May?” Hmm, okay, let’s break this down step by step.
First, in April, Natalia sold clips to 48 of her friends. So, that’s pretty straightforward. She sold to 48 friends, so I think that means she sold 48 clips in April. Yeah, that makes sense. It says “to 48 of her friends,” so each friend bought one clip, so 48 clips total in April.
Then, in May, she sold half as many clips as she did in April. So, if she sold 48 in April, half of that would be… let me calculate that. Half of 48 is 24. So, in May, she sold 24 clips.
Now, the question is asking how many clips she sold altogether in April and May. So, that means I need to add the number she sold in April to the number she sold in May. So, that would be 48 plus 24. Let me add those together. 48 plus 20 is 68, and then plus 4 more is 72. So, 48 plus 24 equals 72.
Wait, let me make sure I didn’t make a mistake. April: 48 clips. May: half of that, so 24. 48 plus 24 is 72. Yeah, that seems right. So, Natalia sold a total of 72 clips in April and May.
…
According to the DeepSeek R1 model card, the model tends to bypass the thinking pattern with certain queries. A relevant finding that was discovered when experimenting with the model generation capabilities, is that it’s possible to make the model bypass the reasoning process in the generation by appending “<think>\n\n</think>” at the end of the prompt.
Example of model output with reasoning bypassing prompt (formatted the model generated tokens for readability):
<|begin▁of▁sentence|><|User|>2 + x = 10 What is the value of x?<|Assistant|><think>\n\n</think>
To find the value of ( x ) in the equation ( 2 + x = 10 ), follow these steps:
- Isolate the variable ( x ) by subtracting 2 from both sides of the equation:
Simplifying both sides gives:
Final Answer: ( )<|end▁of▁sentence|>
The last aspect of the model that is relevant to address in this section are the hidden states. These consist of a tuple of tuples of tensors, where the length of the first tuple is always the same as the number of tokens the model generated (the model’s output sequence without counting the tokens in the input prompt), while the second tuple has a length of 29 (one for the embedding layer and the remaining 28 corresponding to each hidden layer), and finally each tensor have dimensions [batch_size, sequence_length, hidden_size] where hidden_size refers to the size or dimensionality of the hidden layers.
Something important to note is that the value of sequence_length is different for the tensors that are contained in the first element (the one at index zero) of the hidden states. These tensors have a sequence_length value that is equal to the number of tokens in the input prompt, while the rest of tensors have a sequence_length value of one. This is because the implementation of the model is using key-value caching for the autoregressive token generation, so the model is processing the whole input prompt first to generate the first token, then when the second and subsequent tokens are generated, the model only computes the hidden states for that specific token. To better illustrate what was mentioned before, here’s a summary of the exploratory analysis on the hidden states.
Summary of the exploratory analysis on hidden states
| Metric | Value |
|---|---|
| Input token count | 55 |
| Output token count | 455 (400 excluding input tokens) |
| Hidden states output length | 400 |
| Inner hidden states length | 29 |
Inner hidden state dimensions (tensor sizes)
| State Type | Dimensions |
|---|---|
| First state | [1, 55, 1536] |
| Subsequent states | [1, 1, 1536] |
k-Sparse Autoencoder Experiments
EleutherAI’s sparsify library provides functionalities to encode the hidden states of the model per layer using the SAE, and return the top k latent activations along with the indices of the top k features.
It was decided to focus on three layers: 5, 10 and 20 to conduct the experiments, thus obtaining the top 32 latent activations and feature indices per inference and layer. With these top latent activation and feature indices an analysis was performed by obtaining the top feature activations, feature and activation frequencies per layer and model inference, in addition to the top activating tokens per feature, layer and inference.
At first, I attempted to analyze the SAE encoder’s output using the latent activations obtained from encoding all the tokens in the model’s output. However, after plotting the top tokens with the highest activation for several features, it shown what it seems to be an apparent activation “bias” towards the special tokens that appear first in the input prompt: ”<|begin▁of▁sentence|>” and ”<|User|>”.
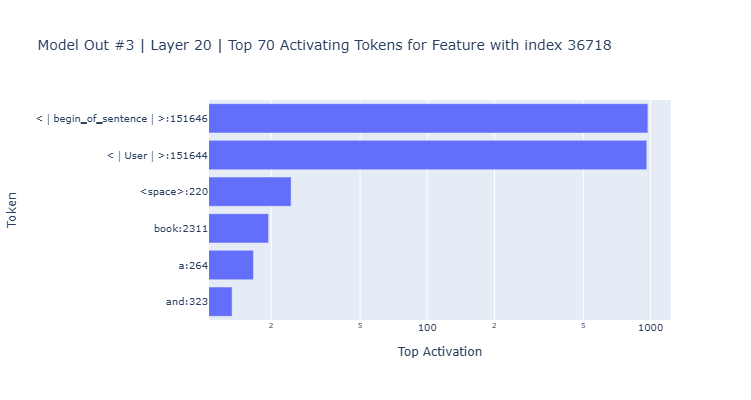
Feature 36718 top activating tokens in layer 20 for model inference #3. High top activation values for the first two special tokens of the input prompt compared to the others.
Because of the large activation values that these tokens consistently have across several model inferences, features and layers, I decided to also analyze the SAE encoding outputs excluding the input prompt hidden states and only focusing on the further generated tokens. This resulted in what I think is a more interpretable relation between the tokens and features activations, besides purely focusing on the tokens the model generated.
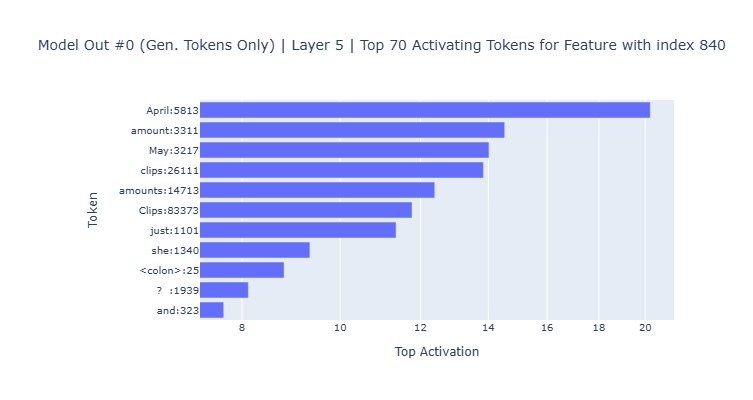
Feature 840 top activating generated only tokens in layer 5 for model inference #0.
Extra Analysis Graphs
In addition to the graphs presented in the key experiments section, there are other plots that were created to analyze the behavior of the top latent activations and feature indices per layer, based on a certain model inference.
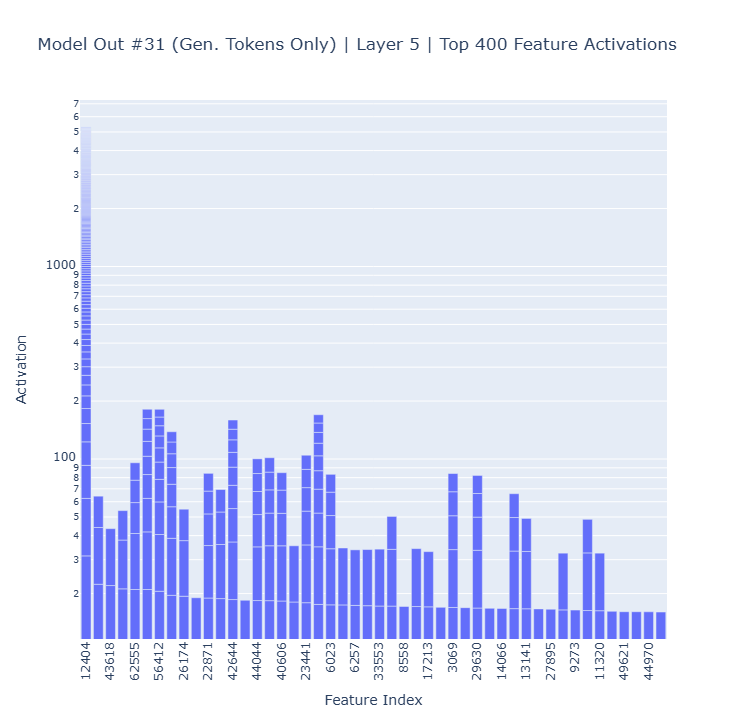
The plot below displays the top 400 feature activations (allowing multiple feature occurrences) of model inference #31 in layer 5. The features show representative activation values, indicating that the SAE can be used to potentially extract and interpret these features.
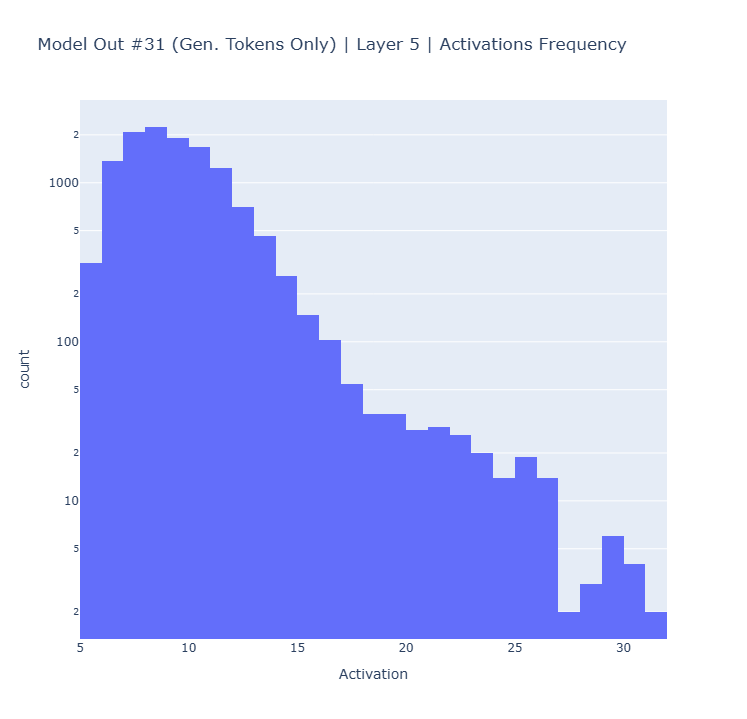
The following plot displays the distribution of the activation frequency with model inference #31 in layer 5. The majority of activation frequencies that were analyzed showed a distribution similar to the one presented here. This shows us that there are commonly few high activation values and the majority of the activation values remain low.
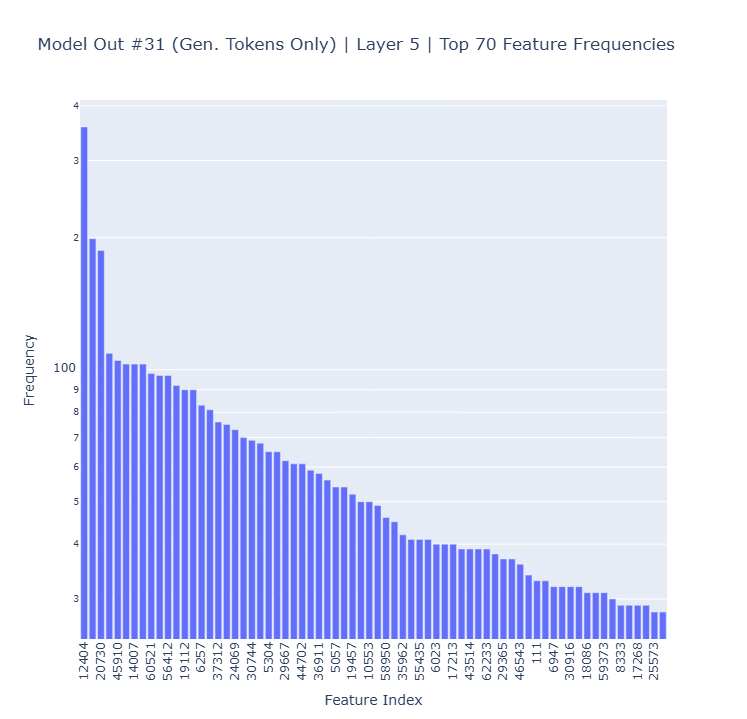
The next plot displays the top feature frequencies with model inference #31 in layer 5. This type of plot enables us to identify which features appear the most with a certain model inference within a specific layer.
The following plot shows a relationship between tokens the model commonly uses after the reasoning process, when it’s ready to describe the method and specify the answer to the input prompt.